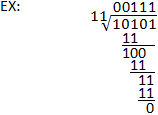Binary Calculator
Use the following calculators to perform the addition, subtraction, multiplication, or division of two binary values, as well as convert binary values to decimal values, and vice versa.
Binary Calculation—Add, Subtract, Multiply, or Divide
Convert Binary Value to Decimal Value
Convert Decimal Value to Binary Value
The binary system is a numerical system that functions virtually identically to the decimal number system that people are likely more familiar with. While the decimal number system uses the number 10 as its base, the binary system uses 2. Furthermore, although the decimal system uses the digits 0 through 9, the binary system uses only 0 and 1, and each digit is referred to as a bit. Apart from these differences, operations such as addition, subtraction, multiplication, and division are all computed following the same rules as the decimal system.
Almost all modern technology and computers use the binary system due to its ease of implementation in digital circuitry using logic gates. It is much simpler to design hardware that only needs to detect two states, on and off (or true/false, present/absent, etc.). Using a decimal system would require hardware that can detect 10 states for the digits 0 through 9, and is more complicated.
Below are some typical conversions between binary and decimal values:
Binary/Decimal Conversion
| Decimal | Binary |
| 0 | 0 |
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 7 | 111 |
| 8 | 1000 |
| 10 | 1010 |
| 16 | 10000 |
| 20 | 10100 |
While working with binary may initially seem confusing, understanding that each binary place value represents 2n, just as each decimal place represents 10n, should help clarify. Take the number 8 for example. In the decimal number system, 8 is positioned in the first decimal place left of the decimal point, signifying the 100 place. Essentially this means:
8 × 100 = 8 × 1 = 8
Using the number 18 for comparison:
(1 × 101) + (8 × 100) = 10 + 8 = 18
In binary, 8 is represented as 1000. Reading from right to left, the first 0 represents 20, the second 21, the third 22, and the fourth 23; just like the decimal system, except with a base of 2 rather than 10. Since 23 = 8, a 1 is entered in its position yielding 1000. Using 18, or 10010 as an example:
18 = 16 + 2 = 24 + 21
10010 = (1 × 24) + (0 × 23) + (0 × 22) + (1 × 21) + (0 × 20) = 18
The step by step process to convert from the decimal to the binary system is:
- Find the largest power of 2 that lies within the given number
- Subtract that value from the given number
- Find the largest power of 2 within the remainder found in step 2
- Repeat until there is no remainder
- Enter a 1 for each binary place value that was found, and a 0 for the rest
Using the target of 18 again as an example, below is another way to visualize this:
| 2n | 24 | 23 | 22 | 21 | 20 |
| Instances within 18 | 1 | 0 | 0 | 1 | 0 |
| Target: 18 | 18 - 16 = 2 | → | 2 - 2 = 0 | ||
Converting from the binary to the decimal system is simpler. Determine all of the place values where 1 occurs, and find the sum of the values.
EX: 10111 = (1 × 24) + (0 × 23) + (1 × 22) + (1 × 21) + (1 × 20) = 23
| 24 | 23 | 22 | 21 | 20 |
| 1 | 0 | 1 | 1 | 1 |
| 16 | 0 | 4 | 2 | 1 |
Hence: 16 + 4 + 2 + 1 = 23.
Binary Addition
Binary addition follows the same rules as addition in the decimal system except that rather than carrying a 1 over when the values added equal 10, carry over occurs when the result of addition equals 2. Refer to the example below for clarification.
Note that in the binary system:
-
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 0, carry over the 1, i.e. 10
EX:
| 10 | 11 | 11 | 10 | 1 | ||
| + | 1 | 0 | 1 | 1 | 1 | |
| = | 1 | 0 | 0 | 1 | 0 | 0 |
The only real difference between binary and decimal addition is that the value 2 in the binary system is the equivalent of 10 in the decimal system. Note that the superscripted 1's represent digits that are carried over. A common mistake to watch out for when conducting binary addition is in the case where 1 + 1 = 0 also has a 1 carried over from the previous column to its right. The value at the bottom should then be 1 from the carried over 1 rather than 0. This can be observed in the third column from the right in the above example.
Binary Subtraction
Similar to binary addition, there is little difference between binary and decimal subtraction except those that arise from using only the digits 0 and 1. Borrowing occurs in any instance where the number that is subtracted is larger than the number it is being subtracted from. In binary subtraction, the only case where borrowing is necessary is when 1 is subtracted from 0. When this occurs, the 0 in the borrowing column essentially becomes "2" (changing the 0-1 into 2-1 = 1) while reducing the 1 in the column being borrowed from by 1. If the following column is also 0, borrowing will have to occur from each subsequent column until a column with a value of 1 can be reduced to 0. Refer to the example below for clarification.
Note that in the binary system:
-
0 - 0 = 0
0 - 1 = 1, borrow 1, resulting in -1 carried over
1 - 0 = 1
1 - 1 = 0
EX1:
| -11 | 20 | 1 | 1 | 1 | ||
| – | 0 | 1 | 1 | 0 | 1 | |
| = | 0 | 1 | 0 | 1 | 0 | |
EX2:
| -11 | 2-10 | 0 | ||
| – | 0 | 1 | 1 | |
| = | 0 | 0 | 1 | |
Note that the superscripts displayed are the changes that occur to each bit when borrowing. The borrowing column essentially obtains 2 from borrowing, and the column that is borrowed from is reduced by 1.
Binary Multiplication
Binary multiplication is arguably simpler than its decimal counterpart. Since the only values used are 0 and 1, the results that must be added are either the same as the first term, or 0. Note that in each subsequent row, placeholder 0's need to be added, and the value shifted to the left, just like in decimal multiplication. The complexity in binary multiplication arises from tedious binary addition dependent on how many bits are in each term. Refer to the example below for clarification.
Note that in the binary system:
-
0 × 0 = 0
0 × 1 = 0
1 × 0 = 0
1 × 1 = 1
EX:
| 1 | 0 | 1 | 1 | 1 | |||
| × | 1 | 1 | |||||
| 1 | 0 | 1 | 1 | 1 | |||
| + | 1 | 0 | 1 | 1 | 1 | 0 | |
| = | 1 | 0 | 0 | 0 | 1 | 0 | 1 |
As can be seen in the example above, the process of binary multiplication is the same as it is in decimal multiplication. Note that the 0 placeholder is written in the second line. Typically the 0 placeholder is not visually present in decimal multiplication. While the same can be done in this example (with the 0 placeholder being assumed rather than explicit), it is included in this example because the 0 is relevant for any binary addition / subtraction calculator, like the one provided on this page. Without the 0 being shown, it would be possible to make the mistake of excluding the 0 when adding the binary values displayed above. Note again that in the binary system, any 0 to the right of a 1 is relevant, while any 0 to the left of the last 1 in the value is not.
EX:
-
1 0 1 0 1 1 0 0
= 0 0 1 0 1 0 1 1 0 0
≠ 1 0 1 0 1 1 0 0 0 0
Binary Division
The process of binary division is similar to long division in the decimal system. The dividend is still divided by the divisor in the same manner, with the only significant difference being the use of binary rather than decimal subtraction. Note that a good understanding of binary subtraction is important for conducting binary division. Refer to the example below, as well as to the binary subtraction section for clarification.