Triangle Calculator
Please provide 3 values including at least one side to the following 6 fields, and click the "Calculate" button. When radians are selected as the angle unit, it can take values such as pi/2, pi/4, etc.
A triangle is a polygon that has three vertices. A vertex is a point where two or more curves, lines, or edges meet; in the case of a triangle, the three vertices are joined by three line segments called edges. A triangle is usually referred to by its vertices. Hence, a triangle with vertices a, b, and c is typically denoted as Δabc. Furthermore, triangles tend to be described based on the length of their sides, as well as their internal angles. For example, a triangle in which all three sides have equal lengths is called an equilateral triangle while a triangle in which two sides have equal lengths is called isosceles. When none of the sides of a triangle have equal lengths, it is referred to as scalene, as depicted below.
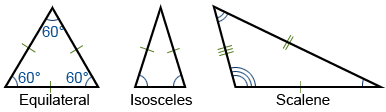
Tick marks on the edge of a triangle are a common notation that reflects the length of the side, where the same number of ticks means equal length. Similar notation exists for the internal angles of a triangle, denoted by differing numbers of concentric arcs located at the triangle's vertices. As can be seen from the triangles above, the length and internal angles of a triangle are directly related, so it makes sense that an equilateral triangle has three equal internal angles, and three equal length sides. Note that the triangle provided in the calculator is not shown to scale; while it looks equilateral (and has angle markings that typically would be read as equal), it is not necessarily equilateral and is simply a representation of a triangle. When actual values are entered, the calculator output will reflect what the shape of the input triangle should look like.
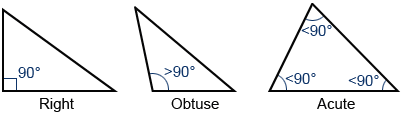
Triangles classified based on their internal angles fall into two categories: right or oblique. A right triangle is a triangle in which one of the angles is 90°, and is denoted by two line segments forming a square at the vertex constituting the right angle. The longest edge of a right triangle, which is the edge opposite the right angle, is called the hypotenuse. Any triangle that is not a right triangle is classified as an oblique triangle and can either be obtuse or acute. In an obtuse triangle, one of the angles of the triangle is greater than 90°, while in an acute triangle, all of the angles are less than 90°, as shown below.
Triangle facts, theorems, and laws
- It is not possible for a triangle to have more than one vertex with internal angle greater than or equal to 90°, or it would no longer be a triangle.
- The interior angles of a triangle always add up to 180° while the exterior angles of a triangle are equal to the sum of the two interior angles that are not adjacent to it. Another way to calculate the exterior angle of a triangle is to subtract the angle of the vertex of interest from 180°.
- The sum of the lengths of any two sides of a triangle is always larger than the length of the third side
- Pythagorean theorem: The Pythagorean theorem is a theorem specific to right triangles. For any right triangle, the square of the length of the hypotenuse equals the sum of the squares of the lengths of the two other sides. It follows that any triangle in which the sides satisfy this condition is a right triangle. There are also special cases of right triangles, such as the 30° 60° 90, 45° 45° 90°, and 3 4 5 right triangles that facilitate calculations. Where a and b are two sides of a triangle, and c is the hypotenuse, the Pythagorean theorem can be written as:
a2 + b2 = c2
EX: Given a = 3, c = 5, find b:
32 + b2 = 52
9 + b2 = 25
b2 = 16
b = 4
- Law of sines: the ratio of the length of a side of a triangle to the sine of its opposite angle is constant. Using the law of sines makes it possible to find unknown angles and sides of a triangle given enough information. Where sides a, b, c, and angles A, B, C are as depicted in the above calculator, the law of sines can be written as shown below. Thus, if b, B and C are known, it is possible to find c by relating b/sin(B) and c/sin(C). Note that there exist cases when a triangle meets certain conditions, where two different triangle configurations are possible given the same set of data.
Given b=2, B=90°, C=45°, find c:
- Given the lengths of all three sides of any triangle, each angle can be calculated using the following equation. Refer to the triangle above, assuming that a, b, and c are known values.
| A = arccos( |
|
) |
| B = arccos( |
|
) |
| C = arccos( |
|
) |
Given a=8, b=6, c=10, find B:
| B = | arccos( |
|
) |
| = | arccos(0.8) = 36.87° |
Area of a Triangle
There are multiple different equations for calculating the area of a triangle, dependent on what information is known. Likely the most commonly known equation for calculating the area of a triangle involves its base, b, and height, h. The "base" refers to any side of the triangle where the height is represented by the length of the line segment drawn from the vertex opposite the base, to a point on the base that forms a perpendicular.
| EX: | 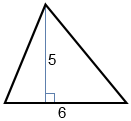 |
Given the length of two sides and the angle between them, the following formula can be used to determine the area of the triangle. Note that the variables used are in reference to the triangle shown in the calculator above. Given a = 9, b = 7, and C = 30°:
| area = |
|
ab × sin(C) |
| = |
|
bc × sin(A) |
| = |
|
ac × sin(B) |
| EX: area = |
|
× 7 × 9 × sin(30°) |
| = |
15.75 |
Another method for calculating the area of a triangle uses Heron's formula. Unlike the previous equations, Heron's formula does not require an arbitrary choice of a side as a base, or a vertex as an origin. However, it does require that the lengths of the three sides are known. Again, in reference to the triangle provided in the calculator, if a = 3, b = 4, and c = 5:
| area = | √s(s - a)(s - b)(s - c) |
|
|
|
|
| area = | √6(6 - 3)(6 - 4)(6 - 5) = 6 |
Median, inradius, and circumradius
Median
The median of a triangle is defined as the length of a line segment that extends from a vertex of the triangle to the midpoint of the opposing side. A triangle can have three medians, all of which will intersect at the centroid (the arithmetic mean position of all the points in the triangle) of the triangle. Refer to the figure provided below for clarification.
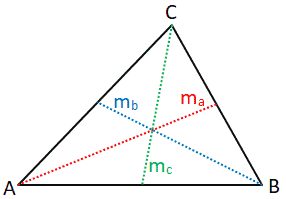
The medians of the triangle are represented by the line segments ma, mb, and mc. The length of each median can be calculated as follows:
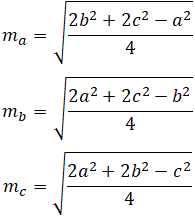
Where a, b, and c represent the length of the side of the triangle as shown in the figure above.
As an example, given that a=2, b=3, and c=4, the median ma can be calculated as follows:
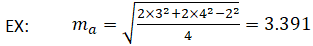
Inradius
The inradius is the radius of the largest circle that will fit inside the given polygon, in this case, a triangle. The inradius is perpendicular to each side of the polygon. In a triangle, the inradius can be determined by constructing two angle bisectors to determine the incenter of the triangle. The inradius is the perpendicular distance between the incenter and one of the sides of the triangle. Any side of the triangle can be used as long as the perpendicular distance between the side and the incenter is determined, since the incenter, by definition, is equidistant from each side of the triangle.
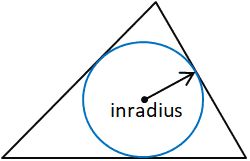
For the purposes of this calculator, the inradius is calculated using the area (Area) and semiperimeter (s) of the triangle along with the following formulas:
where a, b, and c are the sides of the triangle
Circumradius
The circumradius is defined as the radius of a circle that passes through all the vertices of a polygon, in this case, a triangle. The center of this circle, where all the perpendicular bisectors of each side of the triangle meet, is the circumcenter of the triangle, and is the point from which the circumradius is measured. The circumcenter of the triangle does not necessarily have to be within the triangle. It is worth noting that all triangles have a circumcircle (circle that passes through each vertex), and therefore a circumradius.
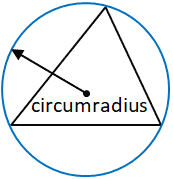
For the purposes of this calculator, the circumradius is calculated using the following formula:
Where a is a side of the triangle, and A is the angle opposite of side a
Although side a and angle A are being used, any of the sides and their respective opposite angles can be used in the formula.




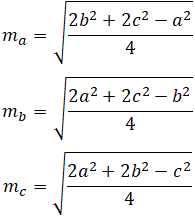
![]()

