Slope Calculator
|
By definition, the slope or gradient of a line describes its steepness, incline, or grade.
Where
m — slope
θ — angle of incline |
 |
If the 2 Points are Known
If 1 Point and the Slope are Known
Slope, sometimes referred to as gradient in mathematics, is a number that measures the steepness and direction of a line, or a section of a line connecting two points, and is usually denoted by m. Generally, a line's steepness is measured by the absolute value of its slope, m. The larger the value is, the steeper the line. Given m, it is possible to determine the direction of the line that m describes based on its sign and value:
- A line is increasing, and goes upwards from left to right when m > 0
- A line is decreasing, and goes downwards from left to right when m < 0
- A line has a constant slope, and is horizontal when m = 0
- A vertical line has an undefined slope, since it would result in a fraction with 0 as the denominator. Refer to the equation provided below.
Slope is essentially the change in height over the change in horizontal distance, and is often referred to as "rise over run." It has applications in gradients in geography as well as civil engineering, such as the building of roads. In the case of a road, the "rise" is the change in altitude, while the "run" is the difference in distance between two fixed points, as long as the distance for the measurement is not large enough that the earth's curvature should be considered as a factor. The slope is represented mathematically as:
| m = |
|
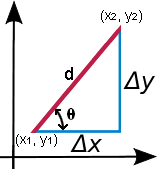
In the equation above, y2 - y1 = Δy, or vertical change, while x2 - x1 = Δx, or horizontal change, as shown in the graph provided. It can also be seen that Δx and Δy are line segments that form a right triangle with hypotenuse d, with d being the distance between the points (x1, y1) and (x2, y2). Since Δx and Δy form a right triangle, it is possible to calculate d using the Pythagorean theorem. Refer to the Triangle Calculator for more detail on the Pythagorean theorem as well as how to calculate the angle of incline θ provided in the calculator above. Briefly:
d = √(x2 - x1)2 + (y2 - y1)2
The above equation is the Pythagorean theorem at its root, where the hypotenuse d has already been solved for, and the other two sides of the triangle are determined by subtracting the two x and y values given by two points. Given two points, it is possible to find θ using the following equation:
m = tan(θ)
Given the points (3,4) and (6,8) find the slope of the line, the distance between the two points, and the angle of incline:
| m = |
|
= |
|
d = √(6 - 3)2 + (8 - 4)2 = 5
|
= tan(θ) |
| θ = tan-1( |
|
) = 53.13° |
While this is beyond the scope of this calculator, aside from its basic linear use, the concept of a slope is important in differential calculus. For non-linear functions, the rate of change of a curve varies, and the derivative of a function at a given point is the rate of change of the function, represented by the slope of the line tangent to the curve at that point.