Probability Calculator

Probability of Two Events

To find out the union, intersection, and other related probabilities of two independent events.

Please input values between 0 and 1.

Probability Solver for Two Events

Please provide any 2 values below to calculate the rest probabilities of two independent events.

Please input values between 0 and 1.

Probability of a Series of Independent Events

Probability of a Normal Distribution

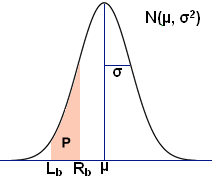
Use the calculator below to find the area P shown in the normal distribution, as well as the confidence intervals for a range of confidence levels.

Probability of Two Events

Probability is the measure of the likelihood of an event occurring. It is quantified as a number between 0 and 1, with 1 signifying certainty, and 0 signifying that the event cannot occur. It follows that the higher the probability of an event, the more certain it is that the event will occur. In its most general case, probability can be defined numerically as the number of desired outcomes divided by the total number of outcomes. This is further affected by whether the events being studied are independent, mutually exclusive, or conditional, among other things. The calculator provided computes the probability that an event A or B does not occur, the probability A and/or B occur when they are not mutually exclusive, the probability that both event A and B occur, and the probability that either event A or event B occurs, but not both.

Complement of A and B

Given a probability A, denoted by P(A), it is simple to calculate the complement, or the probability that the event described by P(A) does not occur, P(A'). If, for example, P(A) = 0.65 represents the probability that Bob does not do his homework, his teacher Sally can predict the probability that Bob does his homework as follows:

P(A') = 1 - P(A) = 1 - 0.65 = 0.35

Given this scenario, there is, therefore, a 35% chance that Bob does his homework. Any P(B') would be calculated in the same manner, and it is worth noting that in the calculator above, can be independent; i.e. if P(A) = 0.65, P(B) does not necessarily have to equal 0.35, and can equal 0.30 or some other number.

Intersection of A and B

The intersection of events A and B, written as P(A ∩ B) or P(A AND B) is the joint probability of at least two events, shown below in a Venn diagram. In the case where A and B are mutually exclusive events, P(A ∩ B) = 0. Consider the probability of rolling a 4 and 6 on a single roll of a die; it is not possible. These events would therefore be considered mutually exclusive. Computing P(A ∩ B) is simple if the events are independent. In this case, the probabilities of events A and B are multiplied. To find the probability that two separate rolls of a die result in 6 each time:

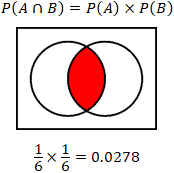
Intersection of A and B

The calculator provided considers the case where the probabilities are independent. Calculating the probability is slightly more involved when the events are dependent, and involves an understanding of conditional probability, or the probability of event A given that event B has occurred, P(A|B). Take the example of a bag of 10 marbles, 7 of which are black, and 3 of which are blue. Calculate the probability of drawing a black marble if a blue marble has been withdrawn without replacement (the blue marble is removed from the bag, reducing the total number of marbles in the bag):

Probability of drawing a blue marble:

P(A) = 3/10

Probability of drawing a black marble:

P(B) = 7/10

Probability of drawing a black marble given that a blue marble was drawn:

P(B|A) = 7/9

As can be seen, the probability that a black marble is drawn is affected by any previous event where a black or blue marble was drawn without replacement. Thus, if a person wanted to determine the probability of withdrawing a blue and then black marble from the bag:

Probability of drawing a blue and then black marble using the probabilities calculated above:

P(A ∩ B) = P(A) × P(B|A) = (3/10) × (7/9) = 0.2333

Union of A and B

In probability, the union of events, P(A U B), essentially involves the condition where any or all of the events being considered occur, shown in the Venn diagram below. Note that P(A U B) can also be written as P(A OR B). In this case, the "inclusive OR" is being used. This means that while at least one of the conditions within the union must hold true, all conditions can be simultaneously true. There are two cases for the union of events; the events are either mutually exclusive, or the events are not mutually exclusive. In the case where the events are mutually exclusive, the calculation of the probability is simpler:

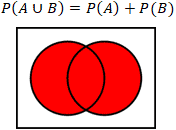
Union of A and B

A basic example of mutually exclusive events would be the rolling of a dice, where event A is the probability that an even number is rolled, and event B is the probability that an odd number is rolled. It is clear in this case that the events are mutually exclusive since a number cannot be both even and odd, so P(A U B) would be 3/6 + 3/6 = 1, since a standard dice only has odd and even numbers.

The calculator above computes the other case, where the events A and B are not mutually exclusive. In this case:

P(A U B) = P(A) + P(B) - P(A ∩ B)

Using the example of rolling dice again, find the probability that an even number or a number that is a multiple of 3 is rolled. Here the set is represented by the 6 values of the dice, written as:

	S = {1,2,3,4,5,6}
Probability of an even number:	P(A) = {2,4,6} = 3/6
Probability of a multiple of 3:	P(B) = {3,6} = 2/6
Intersection of A and B:	P(A ∩ B) = {6} = 1/6
	P(A U B) = 3/6 + 2/6 -1/6 = 2/3

Exclusive OR of A and B

Another possible scenario that the calculator above computes is P(A XOR B), shown in the Venn diagram below. The "Exclusive OR" operation is defined as the event that A or B occurs, but not simultaneously. The equation is as follows:

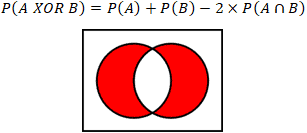
Exclusive OR of A and B

As an example, imagine it is Halloween, and two buckets of candy are set outside the house, one containing Snickers, and the other containing Reese's. Multiple flashing neon signs are placed around the buckets of candy insisting that each trick-or-treater only takes one Snickers OR Reese's but not both! It is unlikely, however, that every child adheres to the flashing neon signs. Given a probability of Reese's being chosen as P(A) = 0.65, or Snickers being chosen with P(B) = 0.349, and a P(unlikely) = 0.001 that a child exercises restraint while considering the detriments of a potential future cavity, calculate the probability that Snickers or Reese's is chosen, but not both:

0.65 + 0.349 - 2 × 0.65 × 0.349 = 0.999 - 0.4537 = 0.5453

Therefore, there is a 54.53% chance that Snickers or Reese's is chosen, but not both.

Normal Distribution

The normal distribution or Gaussian distribution is a continuous probability distribution that follows the function of:

where μ is the mean and σ² is the variance. Note that standard deviation is typically denoted as σ. Also, in the special case where μ = 0 and σ = 1, the distribution is referred to as a standard normal distribution. Above, along with the calculator, is a diagram of a typical normal distribution curve.

The normal distribution is often used to describe and approximate any variable that tends to cluster around the mean, for example, the heights of male students in a college, the leaf sizes on a tree, the scores of a test, etc. Use the "Normal Distribution" calculator above to determine the probability of an event with a normal distribution lying between two given values (i.e. P in the diagram above); for example, the probability of the height of a male student is between 5 and 6 feet in a college. Finding P as shown in the above diagram involves standardizing the two desired values to a z-score by subtracting the given mean and dividing by the standard deviation, as well as using a Z-table to find probabilities for Z. If, for example, it is desired to find the probability that a student at a university has a height between 60 inches and 72 inches tall given a mean of 68 inches tall with a standard deviation of 4 inches, 60 and 72 inches would be standardized as such:

Given μ = 68; σ = 4
(60 - 68)/4 = -8/4 = -2
(72 - 68)/4 = 4/4 = 1

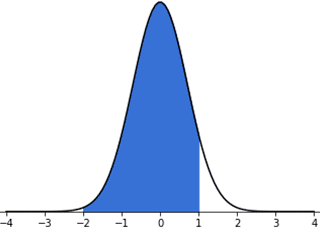
normal distribution example

The graph above illustrates the area of interest in the normal distribution. In order to determine the probability represented by the shaded area of the graph, use the standard normal Z-table provided at the bottom of the page. Note that there are different types of standard normal Z-tables. The table below provides the probability that a statistic is between 0 and Z, where 0 is the mean in the standard normal distribution. There are also Z-tables that provide the probabilities left or right of Z, both of which can be used to calculate the desired probability by subtracting the relevant values.

For this example, to determine the probability of a value between 0 and 2, find 2 in the first column of the table, since this table by definition provides probabilities between the mean (which is 0 in the standard normal distribution) and the number of choices, in this case, 2. Note that since the value in question is 2.0, the table is read by lining up the 2 row with the 0 column, and reading the value therein. If, instead, the value in question were 2.11, the 2.1 row would be matched with the 0.01 column and the value would be 0.48257. Also, note that even though the actual value of interest is -2 on the graph, the table only provides positive values. Since the normal distribution is symmetrical, only the displacement is important, and a displacement of 0 to -2 or 0 to 2 is the same, and will have the same area under the curve. Thus, the probability of a value falling between 0 and 2 is 0.47725 , while a value between 0 and 1 has a probability of 0.34134. Since the desired area is between -2 and 1, the probabilities are added to yield 0.81859, or approximately 81.859%. Returning to the example, this means that there is an 81.859% chance in this case that a male student at the given university has a height between 60 and 72 inches.

The calculator also provides a table of confidence intervals for various confidence levels. Refer to the Sample Size Calculator for Proportions for a more detailed explanation of confidence intervals and levels. Briefly, a confidence interval is a way of estimating a population parameter that provides an interval of the parameter rather than a single value. A confidence interval is always qualified by a confidence level, usually expressed as a percentage such as 95%. It is an indicator of the reliability of the estimate.

Z Table from Mean (0 to Z)

z	0	0.01	0.02	0.03	0.04	0.05	0.06	0.07	0.08	0.09
0	0	0.00399	0.00798	0.01197	0.01595	0.01994	0.02392	0.0279	0.03188	0.03586
0.1	0.03983	0.0438	0.04776	0.05172	0.05567	0.05962	0.06356	0.06749	0.07142	0.07535
0.2	0.07926	0.08317	0.08706	0.09095	0.09483	0.09871	0.10257	0.10642	0.11026	0.11409
0.3	0.11791	0.12172	0.12552	0.1293	0.13307	0.13683	0.14058	0.14431	0.14803	0.15173
0.4	0.15542	0.1591	0.16276	0.1664	0.17003	0.17364	0.17724	0.18082	0.18439	0.18793
0.5	0.19146	0.19497	0.19847	0.20194	0.2054	0.20884	0.21226	0.21566	0.21904	0.2224
0.6	0.22575	0.22907	0.23237	0.23565	0.23891	0.24215	0.24537	0.24857	0.25175	0.2549
0.7	0.25804	0.26115	0.26424	0.2673	0.27035	0.27337	0.27637	0.27935	0.2823	0.28524
0.8	0.28814	0.29103	0.29389	0.29673	0.29955	0.30234	0.30511	0.30785	0.31057	0.31327
0.9	0.31594	0.31859	0.32121	0.32381	0.32639	0.32894	0.33147	0.33398	0.33646	0.33891
1	0.34134	0.34375	0.34614	0.34849	0.35083	0.35314	0.35543	0.35769	0.35993	0.36214
1.1	0.36433	0.3665	0.36864	0.37076	0.37286	0.37493	0.37698	0.379	0.381	0.38298
1.2	0.38493	0.38686	0.38877	0.39065	0.39251	0.39435	0.39617	0.39796	0.39973	0.40147
1.3	0.4032	0.4049	0.40658	0.40824	0.40988	0.41149	0.41308	0.41466	0.41621	0.41774
1.4	0.41924	0.42073	0.4222	0.42364	0.42507	0.42647	0.42785	0.42922	0.43056	0.43189
1.5	0.43319	0.43448	0.43574	0.43699	0.43822	0.43943	0.44062	0.44179	0.44295	0.44408
1.6	0.4452	0.4463	0.44738	0.44845	0.4495	0.45053	0.45154	0.45254	0.45352	0.45449
1.7	0.45543	0.45637	0.45728	0.45818	0.45907	0.45994	0.4608	0.46164	0.46246	0.46327
1.8	0.46407	0.46485	0.46562	0.46638	0.46712	0.46784	0.46856	0.46926	0.46995	0.47062
1.9	0.47128	0.47193	0.47257	0.4732	0.47381	0.47441	0.475	0.47558	0.47615	0.4767
2	0.47725	0.47778	0.47831	0.47882	0.47932	0.47982	0.4803	0.48077	0.48124	0.48169
2.1	0.48214	0.48257	0.483	0.48341	0.48382	0.48422	0.48461	0.485	0.48537	0.48574
2.2	0.4861	0.48645	0.48679	0.48713	0.48745	0.48778	0.48809	0.4884	0.4887	0.48899
2.3	0.48928	0.48956	0.48983	0.4901	0.49036	0.49061	0.49086	0.49111	0.49134	0.49158
2.4	0.4918	0.49202	0.49224	0.49245	0.49266	0.49286	0.49305	0.49324	0.49343	0.49361
2.5	0.49379	0.49396	0.49413	0.4943	0.49446	0.49461	0.49477	0.49492	0.49506	0.4952
2.6	0.49534	0.49547	0.4956	0.49573	0.49585	0.49598	0.49609	0.49621	0.49632	0.49643
2.7	0.49653	0.49664	0.49674	0.49683	0.49693	0.49702	0.49711	0.4972	0.49728	0.49736
2.8	0.49744	0.49752	0.4976	0.49767	0.49774	0.49781	0.49788	0.49795	0.49801	0.49807
2.9	0.49813	0.49819	0.49825	0.49831	0.49836	0.49841	0.49846	0.49851	0.49856	0.49861
3	0.49865	0.49869	0.49874	0.49878	0.49882	0.49886	0.49889	0.49893	0.49896	0.499
3.1	0.49903	0.49906	0.4991	0.49913	0.49916	0.49918	0.49921	0.49924	0.49926	0.49929
3.2	0.49931	0.49934	0.49936	0.49938	0.4994	0.49942	0.49944	0.49946	0.49948	0.4995
3.3	0.49952	0.49953	0.49955	0.49957	0.49958	0.4996	0.49961	0.49962	0.49964	0.49965
3.4	0.49966	0.49968	0.49969	0.4997	0.49971	0.49972	0.49973	0.49974	0.49975	0.49976
3.5	0.49977	0.49978	0.49978	0.49979	0.4998	0.49981	0.49981	0.49982	0.49983	0.49983
3.6	0.49984	0.49985	0.49985	0.49986	0.49986	0.49987	0.49987	0.49988	0.49988	0.49989
3.7	0.49989	0.4999	0.4999	0.4999	0.49991	0.49991	0.49992	0.49992	0.49992	0.49992
3.8	0.49993	0.49993	0.49993	0.49994	0.49994	0.49994	0.49994	0.49995	0.49995	0.49995
3.9	0.49995	0.49995	0.49996	0.49996	0.49996	0.49996	0.49996	0.49996	0.49997	0.49997
4	0.49997	0.49997	0.49997	0.49997	0.49997	0.49997	0.49998	0.49998	0.49998	0.49998

Probability of A: P(A)
Probability of B: P(B)
Probability of A NOT occuring: P(A')
Probability of B NOT occuring: P(B')
Probability of A and B both occuring: P(A∩B)
Probability that A or B or both occur: P(A∪B)
Probability that A or B occurs but NOT both: P(AΔB)
Probability of neither A nor B occuring: P((A∪B)')

	Probability	Repeat Times
Event A
Event B

Mean: (µ)
Standard Deviation (σ):
Left Bound (L_b):		For negative infinite, use -inf
Right Bound (R_b):		For positive infinite, use inf