Pythagorean Theorem Calculator
Please provide any 2 values below to solve the Pythagorean equation: a2 + b2 = c2.
Pythagorean Theorem
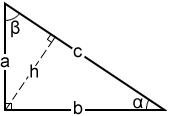
The Pythagorean Theorem, also known as Pythagoras' theorem, is a fundamental relation between the three sides of a right triangle. Given a right triangle, which is a triangle in which one of the angles is 90°, the Pythagorean theorem states that the area of the square formed by the longest side of the right triangle (the hypotenuse) is equal to the sum of the area of the squares formed by the other two sides of the right triangle:
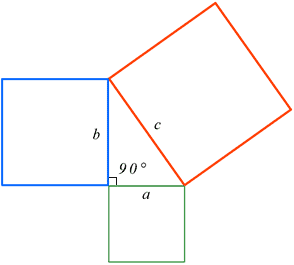
In other words, given that the longest side c = the hypotenuse, and a and b = the other sides of the triangle:
a2 + b2 = c2
This is known as the Pythagorean equation, named after the ancient Greek thinker Pythagoras. This relationship is useful because if two sides of a right triangle are known, the Pythagorean theorem can be used to determine the length of the third side. Referencing the above diagram, if
a = 3 and b = 4
the length of c can be determined as:
c = √a2 + b2 = √32+42 = √25 = 5
It follows that the length of a and b can also be determined if the lengths of the other two sides are known using the following relationships:
a = √c2 - b2
b = √c2 - a2
The law of cosines is a generalization of the Pythagorean theorem that can be used to determine the length of any side of a triangle if the lengths and angles of the other two sides of the triangle are known. If the angle between the other sides is a right angle, the law of cosines reduces to the Pythagorean equation.
There are a multitude of proofs for the Pythagorean theorem, possibly even the greatest number of any mathematical theorem.
Algebraic proof:
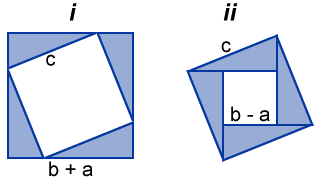
In the figure above, there are two orientations of copies of right triangles used to form a smaller and larger square, labeled i and ii, that depict two algebraic proofs of the Pythagorean theorem.
In the first one, i, the four copies of the same triangle are arranged around a square with sides c. This results in the formation of a larger square with sides of length b + a, and area of (b + a)2. The sum of the area of these four triangles and the smaller square must equal the area of the larger square such that:
| (b + a)2 = c2 + 4 |
| = c2 + 2ab |
which yields:
| c2 = | (b + a)2 - 2ab |
| = | b2 + 2ab + a2 - 2ab |
| = | a2 + b2 |
which is the Pythagorean equation.
In the second orientation shown in the figure, ii, the four copies of the same triangle are arranged such that they form an enclosed square with sides of length b - a, and area (b - a)2. The four triangles with area
| ab |
| 2 |
| (b - a)2 + 2ab | ||||||
| = | b2 - 2ab + a2 + 2ab | ||||||
| = | a2 + b2 |
Since the larger square has sides c and area c2, the above can be rewritten as:
c2 = a2 + b2
which is again, the Pythagorean equation.
There are numerous other proofs ranging from algebraic and geometric proofs to proofs using differentials, but the above are two of the simplest versions.