Area Calculator
The following are calculators to evaluate the area of seven common shapes. The area of more complex shapes can usually be obtained by breaking them down into their aggregating simple shapes, and totaling their areas. This calculator is especially useful for estimating land area.
Rectangle
Triangle
Use the Triangle Calculator to determine |
Trapezoid
Circle
 |
Sector
 |
Ellipse
 |
Parallelogram
Area is a quantity that describes the size or extent of a two-dimensional figure or shape in a plane. It can be visualized as the amount of paint that would be necessary to cover a surface, and is the two-dimensional counterpart of the one-dimensional length of a curve, and three-dimensional volume of a solid. The standard unit of area in the International System of Units (SI) is the square meter, or m2. Provided below are equations for some of the most common simple shapes, and examples of how the area of each is calculated.
Rectangle
A rectangle is a quadrilateral with four right angles. It is one of the simplest shapes, and calculating its area only requires that its length and width are known (or can be measured). A quadrilateral by definition is a polygon that has four edges and vertices. In the case of a rectangle, the length typically refers to the longer two edges of the quadrilateral, while the width refers to the shorter of the two edges. When the length and width of a rectangle are equal, the shape is a special case of a rectangle, called a square. The equation for calculating the area of a rectangle is as follows:
area = length × width
The Farmer and his Daughter – Unsold Land
Imagine a farmer trying to sell a piece of land that happens to be perfectly rectangular. Because he owns some cows that he did not want frolicking freely, he fenced the piece of land and knew the exact length and width of each edge. The farmer also lives in the United States, and being unfamiliar with the use of SI units, still measures his plot of land in terms of feet. The foot was defined to be exactly 0.3048 meters in 1959 after having changed over an extensive period of time, as historically, the human body was often used to provide a basis for units of length, and unsurprisingly, was inconsistent based on time and location. Tangent aside, the farmer's plot of land has a length of 220 feet, and a width of 99 feet. Using this information:
area = 220 × 99 = 21780 sq ft
The farmer's plot of land, which has an area of 21,780 square feet, equates to half an acre, where an acre is defined as the area of 1 chain by 1 furlong, which is defined by something else, and so on, and is why SI now exists. Unfortunately for the farmer, he lives in an area predominated by foreign investors with smaller feet, who felt that they should be getting more square feet for their money, and his land remains unsold today.
Triangle
There are many equations for calculating the area of a triangle based on what information is available. As mentioned in the calculator above, please use the Triangle Calculator for further details and equations for calculating the area of a triangle, as well as determining the sides of a triangle using whatever information is available. Briefly, the equation used in the calculator provided above is known as Heron's formula (sometimes called Hero's formula), referring to the Hero of Alexandria, a Greek mathematician and engineer considered by some to be the greatest experimenter of ancient times. The formula is as follows:
area = √s(s - x)(s - y)(s - z)
| where: |
|
|||||
| x, y, z are the sides of the triangle |
The Farmer and his Daughter - Triangle Daze
At this point in time, through extreme effort and perseverance, the farmer has finally sold his 21,780 sq ft plot of land and has decided to use some of the money earned to build a pool for his family. Unfortunately for the farmer, he does not consider the fact that the maintenance costs of a pool for one year alone could likely pay for his children to visit any pool or water theme park for years to come. Even more unfortunately for the farmer, his 7-year-old daughter who has recently traveled to Egypt vicariously through Dora the Explorer, has fallen in love with triangles, and insists that the pool not only be triangular in shape, but also that the measurements must only include the number 7, to represent her age and immortalize this point of her life in the form of a triangular pool. Being a doting father, the farmer acquiesces to his daughter's request and proceeds to plan the construction of his triangular pool. The farmer must now determine whether he has sufficient area in his backyard to house a pool. While the farmer has begun to learn more about SI units, he is as yet uncomfortable with their use and decides that his only viable option is to construct a pool in the form of an equilateral triangle with sides 77 ft in length, since any other variation would either be too large or small. Given these dimensions, the farmer determines the necessary area as follows:
| s = |
|
= 115.5 |
area = √115.5 × (115.5 - 77)3 = 2567.33 sq ft
Since the longest distance between any two points of an equilateral triangle is the length of the edge of the triangle, the farmer reserves the edges of the pool for swimming "laps" in his triangular pool with a maximum length approximately half that of an Olympic pool, but with double the area – all under the watchful eyes of the presiding queen of the pool, his daughter, and the disapproving glare of his wife.
Trapezoid
A trapezoid is a simple convex quadrilateral that has at least one pair of parallel sides. The property of being convex means that a trapezoid's angle does not exceed 180° (in contrast, a concave quadrilateral would), while being simple reflects that trapezoids are not self-intersecting, meaning two non-adjacent sides do not cross. In a trapezoid, the parallel sides are referred to as the bases of the trapezoid, and the other two sides are called the legs. There exist more distinctions and classifications for different types of trapezoids, but their areas are still calculated in the same manner using the following equation:
| area = |
|
× h |
The Farmer and his Daughter – Ramping Endeavors
Two years have passed since the farmer's pool was completed, and his daughter has grown and matured. While her love for triangles still persists, she eventually came to the realization that no matter how well-"triangled" she was, triangles alone cannot make the world go round, and that Santa's workshop could not plausibly balance on the North Pole, were the world a pyramid rather than a sphere. Slowly, she has begun to accept other shapes into her life and pursues her myriad different interests – currently freestyle BMX. As such, she requires a ramp, but unfortunately for the farmer, not just any ramp. The ramp must be comprised of only shapes that can be formed using multiple triangles, since, like her rap idol B.o.B, the farmer's daughter still has difficulty accepting the reality of curved surfaces. It must, of course, also only use the number 9 in its measurements to reflect her age. The farmer decides that his best option is to build a ramp comprised of multiple rectangles, with the side face of the ramp being in the shape of a trapezoid. As the farmer has now become more comfortable with SI, he is able to be more creative with his use of units, and can build a more reasonably sized ramp while adhering to his daughter's demands. He decides to build a ramp with a trapezoidal face with a height of 9 ft, a bottom base of length 29.528 ft (9 m), and a top base of 9 ft. The area of the trapezoid is calculated as follows:
| area = |
|
× 9 = 173.376 sq ft |
Circle
A circle is a simple closed shape formed by the set of all points in a plane that are a given distance from a given center point. This distance from the center to any point on the circle is called the radius. More detail can be found regarding circles on the Circle Calculator page, but to calculate the area, it is only necessary to know the radius, and understand that values in a circle are related through the mathematical constant π. The equation for calculating the area of a circle is as follows:
area = πr2
The Farmer and his Daughter – Circle of Li(f)es
Another six years have passed, and his daughter has grown into a strong, beautiful, powerful, confident 15-year-old ingrate solely focused on seeking external validation from acquaintances and strangers on social media while wholeheartedly ignoring genuine support from immediate family and friends. Having had an argument with her father about her excessive use of social media, she decides to prey on her father's fear of the unknown, and belief in the supernatural in order to prank him. Not knowing where to start, she walks around town talking to a variety of strangers all of whom seemingly have endless founts of wisdom and advice, where she learns about crop circles and their association with aliens and unidentified flying objects as well as many other topics that ignore all scientific and logical explanations. Having finally been convinced of the spherical nature of the Earth, deleted all her past social media posts relating to B.o.B, and expanded her love of triangles to an acceptance of other shapes, she decides to make a basic crop circle consisting of a number of concentric circles, and wants to determine the area necessary to create a crop circle with an outer radius of 15 ft. She does so using the following equation:
area = π × 152 = 706.858 sq ft
Unfortunately for the farmer, not only is he terrified of the crop circle that appeared overnight on the night that his daughter told him she was at a slumber party with her friends, that for some odd reason did not result in superfluous Instagram posts (he was of course his daughter's first follower), but the number of "circle investigators" and "cereologists" showing up on his farm to examine, and subsequently confirm the authenticity of the crop circle as an alien construction, cost him significant damages to his crops.
Sector
A sector of a circle is essentially a proportion of the circle that is enclosed by two radii and an arc. Given a radius and an angle, the area of a sector can be calculated by multiplying the area of the entire circle by a ratio of the known angle to 360° or 2π radians, as shown in the following equation:
| area = |
|
× πr2 | if θ is in degrees |
or
| area = |
|
× πr2 | if θ is in radians |
The Farmer and his Daughter – Sectioning Family
The farmer and his family are facing their most significant dilemma to date. One year has passed, and the farmer's daughter is now 16 years old and as part of her birthday celebration, her mother baked her favorite dessert, blackberry pie. Unfortunately for the farmer's daughter, blackberry pie also happens to be a favorite food of their pet raccoon, Platypus, as evidenced by 180° worth of the pie being missing with telltale signs of the culprit in the form of crumbs leading towards the overindulgent raccoon. Initially, the pie would easily have been split between three people and one raccoon, but now, half the pie has to be divided between three people as a chagrined, but satiated Platypus watches from a distance. Given that each person will receive 60° worth of the pie with a radius of 16 inches, the area of pie that each person receives can be calculated as follows:
area= 60°/360° × π × 162 = 134.041 in2
As a result of Platypus' inconsideration, each person gets one-third less pie, and the daughter contemplatively recalls American history class, where she learned about the Battle of the Alamo and the portrayal of the folk hero Davy Crockett and his coonskin hat.
Ellipse
An ellipse is the generalized form of a circle, and is a curve in a plane where the sum of the distances from any point on the curve to each of its two focal points is constant, as shown in the figure below, where P is any point on the ellipse, and F1 and F2 are the two foci.

When F1 = F2, the resulting ellipse is a circle. The semi-major axis of an ellipse, as shown in the figure that is part of the calculator, is the longest radius of the ellipse, while the semi-minor axis is the shortest. The major and minor axes refer to the diameters rather than radii of the ellipse. The equation for calculating the area of an ellipse is similar to that for calculating the area of a circle, with the only difference being the use of two radii, rather than one (since the foci are in the same location for a circle):
area = πab
where a and b are the semi-major
and semi-minor axes
The Farmer and his Daughter – Falling out of Orbit
Two years have passed since the mysterious disappearance of the family pet, Platypus, and the farmer's daughter's fortuitous winning of a furry accessory through the school lottery that helped fill the void of the loss of their beloved pet. The farmer's daughter is now 18 and is ready to escape rural Montana for a college life replete with freedom and debauchery, and of course some learning on the side. Unfortunately for the farmer's daughter, she grew up in an environment brimming with positive reinforcement, and subsequently, the mentality that one should "shoot for the moon [since] even if you miss, you'll land among the stars," as well as the assertion from everyone around her that she could do absolutely anything she put her mind to! As such, with her suboptimal grades, lack of any extracurricular activities due to her myriad different interests consuming all of her free time, zero planning, and her insistence on only applying to the very best of the best universities, the shock that resulted when she was not accepted to any of the top-tier universities she applied to could be reasonably compared to her metaphorically landing in deep space, inflating, freezing, and quickly suffocating when she missed the moon and landed among the stars. Along with her lungs, her dream of becoming an astrophysicist was summarily ruptured, at least for the time being, and she was relegated to calculating the elliptical area necessary in her room to build a human sized model of Earth's near elliptical orbit around the sun, so she could gaze longingly at the sun in the center of her room and its personification of her heart, burning with passion, but surrounded by the cold vastness of space, with the Earth's distant rotation mockingly representing the distance between her dreams, and solid ground.
area = π × 18 ft × 20 ft= 1130.97 sq ft
Parallelogram
A parallelogram is a simple quadrilateral which has two pairs of parallel sides, where the opposite sides and angles of the quadrilateral have equal lengths and angles. Rectangles, rhombuses, and squares are all special cases of parallelograms. Remember that the classification of a "simple" shape means that the shape is not self-intersecting. A parallelogram can be divided into a right triangle and a trapezoid, which can further be rearranged to form a rectangle, making the equation for calculating the area of a parallelogram essentially the same as that for calculating a rectangle. Instead of length and width however, a parallelogram uses base and height, where the height is the length of the perpendicular between a pair of bases. Based on the figure below, the equation for calculating the area of a parallelogram is as follows:
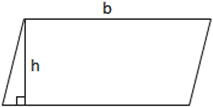
area = b × h
The Farmer and his Daughter – Diamond in the Sky
Another two years have passed in the life of the farmer and his family, and though his daughter had been a cause for intense worry, she has finally bridged the distance between the blazing sun that is her heart, and the Earth upon which society insists she must remain grounded. Through the struggles that ensued from her self-imposed isolation, surrounded by imagined, judgmental eyes presuming her failure from all directions, the farmer's daughter emerged from the pressures of the Earth like a diamond, shining brightly and firm in her resolve. Despite all its drawbacks, she decides that there is little choice but to persist through the asteroid field of life in hopes that a Disney fairy tale ending exists. At long last, fortunately for the farmer's daughter and her family, hope does appear, but not in the form of a Prince Charming, but rather as a sign from the supposed heavens. Through all of her metaphorical musings and tribulations involving space, it almost becomes believable that the farmer's daughter somehow influenced the massive octahedral diamond asteroid falling squarely, but safely upon their farmland, which she interprets as representing her journey, formation, and eventual homecoming. The farmer's daughter proceeds to measure the area of one of the rhomboidal faces of her newly found symbol of life:
area = 20 ft × 18 ft = 360 sq ft
Unfortunately for the farmer's daughter, the appearance of the enormous diamond drew attention from all over the world, and after sufficient pressure, she succumbs to the human within her, and sells the diamond, the very representation of her life and soul, to a wealthy collector, and proceeds to live the rest of her life in lavish indulgence, abandoning her convictions, and losing herself within the black hole of society.
Common Area Units
| Unit | Area in m2 |
| square meter | SI Unit |
| hectare | 10,000 |
| square kilometre (km2) | 1,000,000 |
| square foot | 0.0929 |
| square yard | 0.8361 |
| acre | 4,046.9 (43,560 square feet) |
| square mile | 2,589,988 (640 acres) |